Auswertung der Ergebnisse von Online-Umfragen:
Deskriptive Statistiken Tabellen, Diagrammen, Deskriptive Statistiken

Im Zuge der Auswertung von Online- Umfragen muss man sich mit deskriptiver Statistik befassen. Darunter versteht man das Zusammenfassen von Daten zu anschaulichen Grafiken beziehungsweise zu aussagefähigen Kennzahlen. Das Ziel ist es also aus den unübersichtlichen gesammelten Daten eine einzige einfache Lösung zu erhalten, was das präsentieren und forschen von Umfragen enorm vereinfacht.
QUESTIONSTAR bietet eine Vielzahl an Instrumenten der deskriptiven Statistik um diese gesammelten Daten aussagekräftig als einfache Lösung darzustellen.
Die Berichts und Analysefunktion des Tools lässt sich bequem auf dem Dashboard abrufen, wenn man bei einer erstellten Umfrage auf das Options Symbol oben rechts klickt.
Anschließend wählt man Ergebnisse auswerten aus. Die Auswertung und Analyse der Umfrage erfolgt automatisch. Über das Zahnradsymbol kann nun zwischen vielen verschiedenen Visualisierungsarten entschieden werden.

Im folgenden werden auf die Visualisierungsarten eingegangen.
Zunächst gilt es, die wichtigsten statistischen Grundbegriffe zu erläutern.
Lagemaße
Lagemaße geben den Mittelwert von erhobenen Daten wieder. Sie sind ein Maß für das Zentrum einer Verteilung.
Die drei wichtigsten Lagemaße sind das arithmetische Mittel, der Modus und der Median.
Das arithmetische Mittel
Mit dem arithmetischen Mittel lassen sich die Mittelwerte von allen quantitativen Daten wie beispielsweise Preise oder Körpergrößen ermitteln.
Berechnet wird er indem man die gesammelten Werte x1, x2, x3… xn addiert und durch die Anzahl n der Beobachtungen dividiert.
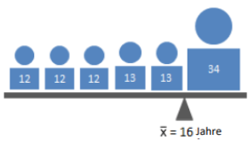
Beispiel: Von 6 Kindern sind 3 Kinder 12 und die anderen 3 Kinder sind 13 Jahre Alt
( (12+12+12+13+13+13) / 6 ) = 12,5 Jahre
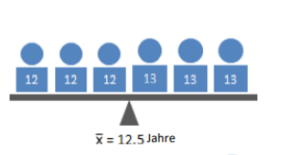
Jedoch ist zu erwähnen, dass das arithmetische Mittel anfällig für Ausreißer, also auf Stichproben mit stark variierenden Daten ist.
Der Modus
Der Modus ist das Merkmal, welches am häufigsten auftritt. Im Säulendiagramm kann man ihn besonders einfach ablesen, da er die längste Säule aufweist.
| Körpergröße in cm | 1,90 | 1,70 | 1,85 | 1,64 | 1,73 |
| Häufigkeit | 4 | 1 | 3 | 1 | 2 |
In dieser Befragung, bei der 11 Probanden nach ihrer Körpergröße gefragt wurden, ist der Modus bei 1,90cm mit einer absoluten Häufigkeit von 4.
Der Median
Der Median beschreibt den zentralen Wert der genau in der Mitte der gesammelten Daten ist. Hierfür werden die Daten der größe nach geordnet so dass 50% der Daten kleiner und 50% größer als der Median ist.
Bei ungeraden Datenwerten liegt der Median in der Mitte. Bei geraden Datenwerten ist der Median der Durchschnitt der beiden mittleren Werte.
(1,64) (1,70) (1,73) (1,73) (1,85) (1,85) (1,85) (1,90) (1,90) (1,90) (1,90)
In dem Fall ist der Median bei 1,85 cm. Diese Körpergröße liegt in der Mitte.
Welches Lagemaß sinnvoll ist hängt von der Art des Skalenniveaus ab. Man unterscheidet zwischen Nominal, Ordinal und Metrisch.
Nominal skalierte Daten sind Daten, die in keine natürliche Reihenfolge festgelegt werden können. Typische Nominalskalierte Daten sind zum Beispiel das Geschlecht der Probanden. Als Lagemaß ist daher nur der Modus sinnvoll.
Ordinal skalierte Daten können in eine natürliche Reihenfolge eingeordnet werden, allerdings können die Abstände zwischen den einzelnen Rängen nicht miteinander verglichen werden, da sie nicht quantifiziert sind. Ein Beispiel für Ordinalskalierte Daten ist die Frage nach der Zufriedenheit auf einer Skala von 1 bis 10. Als Lagemaß ist der Modus und der Median sinnvoll.
Metrisch skalierte Daten haben eine natürliche Reihenfolge und quantifizierbare Abstände. Ein Beispiel hierfür ist das Alter der Probanden (21 Jahre, 22 Jahre …). Hier können alle drei Lagemaße angewendet werden.
Weitere wichtigen Grundbegriffe erfolgen anhand eines Beispiels.
Unter der Grundgesamtheit versteht man beispielsweise alle Wahlberechtigten in Deutschland.
Eine Stichprobe sind davon zufällig ausgewählte Wahlberechtigte.
Merkmalsträger sind alle befragten Wahlberechtigten.
Das Merkmal ist die bevorzugte Partei der Merkmalsträger und die
Merkmalsausprägung ist die jeweilige Partei, also zum Beispiel CDU, SPD, FDP …
Visualisierungsarten von QUESTIONSTAR
Nun betrachten wir die verschiedenen Visualisierungsarten von QUESTIONSTAR.
Tabellarische Zusammenfassung
Absolute Häufigkeiten und relative Häufigkeiten
Bei einer fiktiven Umfrage wurden 10 Teilnehmer befragt:
“Welche Art von Alkohol bevorzugen Sie?”
Folgende 10 Merkmalsausprägungen wurden erhalten:
Bier, Bier, Wein, Whisky, Bier, Wodka, Bier, Wodka, Wodka, Wein
Klassische Häufigkeitstabellen liefern einen klaren Überblick über die gesammelten Daten einer Online Umfrage.
| Merkmalsausprägung | absolute Häufigkeit H |
relative Häufigkeit h |
kumulierte Häufigkeit h* |
| Bier | 4 | 0,4 | 0,4 |
| Wein | 2 | 0,2 | 0,6 |
| Whisky | 1 | 0,1 | 0,7 |
| Wodka | 3 | 0,3 | 1 |
| ∑ 10 |
Die absolute Häufigkeit gibt an, wie oft der jeweilige gemessene Wert in den Daten vorkommt. In dem Beispiel von oben sind es also für Bier 4, für Wein 2, Whisky 1 und für Wodka 3.
Die relative Häufigkeit setzt nun diese Werte ins Verhältnis zur Summe aller Häufigkeiten. Daraus ergeben sich dann prozentuale Anteile für die jeweiligen Werte. Man berechnet also 4 durch 10 und erhält somit für Bier einen relativen Anteil von 0,4 beziehungsweise 40%.
Manchmal gibt es zu viele Werte, um für jeden Wert eine Zeile zu erstellen. In diesem Fall müssen wir mehrere Werte zu Gruppen zusammenfassen. Beispielsweise könnte man bei der Befragung nach dem Alter der Probanden das Alter in Kategorien wie (<30) (30-40) und (>40) einteilen.
Grafische Darstellung
Säulendiagramm und Balkendiagramm
Eine weitere Möglichkeit gesammelte Daten zu präsentieren sind Grafiken. Diese eignen sich besonders gut dafür, die Daten in einer Präsentation zu vermitteln. Säulendiagramme und Balkendiagramme sind prinzipiell gleich. Sie unterscheiden sich lediglich je nach Ausrichtung der Rechtecke. Bei einem Säulendiagramm sind sie horizontal und bei einem Balkendiagramm vertikal. Die Höhen beim Säulendiagramm und die Breite beim Balkendiagramm können entweder absolute oder relative Häufigkeiten sein. Entscheidend ist, dass die Länge jedes Rechtecks der darzustellenden Häufigkeit entspricht.
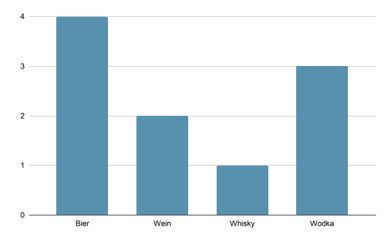
Abbildung eines Säulendiagramms
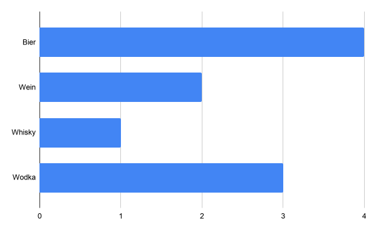
Abbildung eines Balkendiagramms
Kreisdiagramm
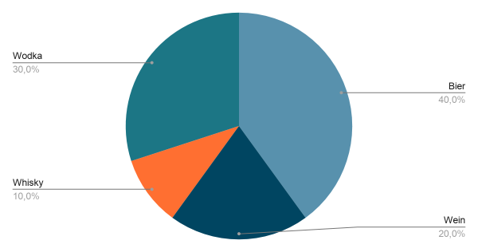
Das Kreisdiagramm ist eine kreisförmige Darstellungsform, bei der die Verteilungen der Häufigkeiten in verschiedene Sektoren unterteilt wird. Es sollte immer die prozentuale relative Häufigkeit angeben, mit der entsprechenden Beschriftung.
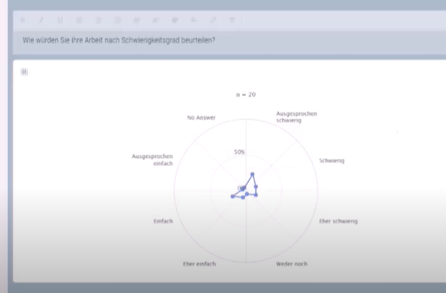
Radardiagramm
Auch das Radardiagramm ist kreisförmig. Um dem Kreis herum stehen die vorher frei festgelegten verschiedenen Antwortmöglichkeiten. Bei steigender Häufigkeit derselben Antwortmöglichkeiten werden die Punkte jeweils näher in die jeweilige Richtung ausgebreitet. Je geringer die Häufigkeit, desto weiter ist der Punkt entfernt. Insgesamt werden die Punkte klassischerweise durch Linien verbunden, wodurch eine Fläche entsteht.
Das Radardiagramm eignet sich ideal dafür Erkenntnisse, Meinungen und Haltungen der Probanden auf einem Blick einschätzen zu können.
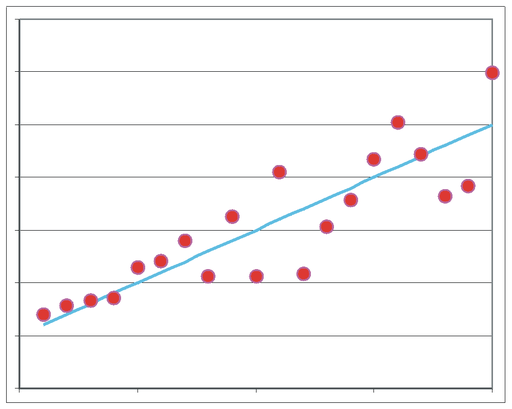
Streudiagramme
Streudiagramme halten fest, in welchem Verhältnis sich zwei Größen in einem Zusammenhang zueinander bewegen. Veranschaulicht wird dies in einem Koordinatensystem, wobei jede Achse für eine Größe steht. Außerdem kann er feststellen, inwieweit eine Abweichung zum Durchschnitt vorliegt.
Boxplots
Ein Boxplots ist ebenfalls ein Diagramm welches dazu dient, Streuung sichtbar darzustellen. Bestandteile eines Boxplots sind: Minimum, Unteres Quartil, Median, Oberes Quartil, Maximum.
Als Beispiel dient folgender exemplarischer Datensatz.
2, 2,2,3,3,3,4, 4, 5,5,6,6,7,7, 8
Minimum Unteres Quartil Median Oberes Quartil Maximum
Die Box setzt sich aus den beiden Quartilen zusammen, die mit dem Minimum und Maximum durch zwei Linien verbunden werden.
Das Minimum und das Maximum geben jeweils den kleinsten und den größten Wert im Boxplot wieder. Die Quartile geben jeweils an, wieviel Prozent der Daten größer oder kleiner als ein bestimmter Wert sind. Der Median wird als vertikaler Strich in der Box vermerkt.
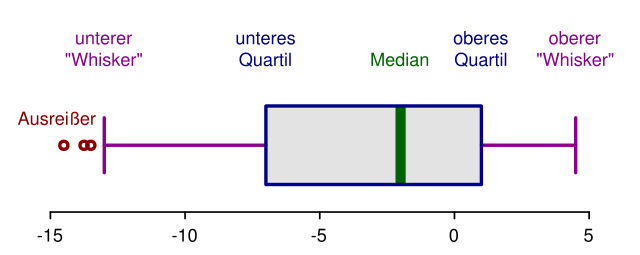
Symbolbild eines Boxplots
Wordcloud
Die Wordcloud sind Ansammlungen von Schlagwörtern und eignen sich am besten, wenn Probanden nach Verbesserungsvorschlägen gefragt werden. Durch die Größe der Wörter erfahren wir grafisch, welche Wörter am häufigsten bei den Antworten verwendet worden sind. Je öfter desto größer werden die Wörter. Anders als bei einem Fließtext erhält man bei der Wordcloud einen schnellen Überblick über die wichtigsten Schlagwörter, was dabei hilft Zusammenhänge zu verdeutlichen.

Hat man sich für seine präferierten Visualisierungs Arten festgelegt, so lässt sich über das Augensymbol oben rechts eine Vorschau des fertigen Datenanalyse-Berichts anzeigen.
Der gesamte Bericht lässt sich einfach durch den Button “Bericht exportieren” in verschiedene Datenformate formatieren und runterladen. Damit endet die Datenanalyse und der Bericht steht nun für die Präsentation zur Verfügung!
Autor:
Sivan Karatas