Zufallsstichproben
In diesem Artikel geht es um Zufallsstichproben. Es werden Hinweise gegeben, weshalb es wichtig ist, die Stichproben zufällig zu ziehen. Außerdem wird erläutert, wie man eine solche Zufallsstichprobe durchführt. Dabei werden die einfache Zufallsstichprobe und die systematische Zufallsstichprobe betrachtet.
Der wohl berühmteste Schlagzeilenfehler der Welt
 Geschichtskenner oder gelernte Journalisten werden dieses Bild sofort wiedererkennen:
Geschichtskenner oder gelernte Journalisten werden dieses Bild sofort wiedererkennen:
Der wohl berühmteste Fehler einer Zeitung, der durch Voreingenommenheit und einer fehlerbehafteten Meinungsumfrage resultierte. Denn die Historiker unter uns wissen genau – Truman hat die Wahl um das höchste Amt der Welt gewonnen, nicht Dewey.
Hätten die Statistiker der “Chicago Daily Tribute” ihre Stichproben zufällig ausgewählt, wäre ihnen diese Peinlichkeit bestimmt erspart geblieben.
Damit dir nicht das Gleiche passiert, und du immer repräsentative Umfragen zur Präsidentenwahl und noch vielen mehr stellen kannst, verschafft dir dieser Artikel einen guten Überblick zum Thema Zufallsstichproben.
Wiederholung der Grundbegriffe
Wenn du dich gerade fragst, was so eine Stichprobe überhaupt ist – kein Problem. Wir fangen zuerst mit den Grundbegriffen an.
Kurzgesagt: Eine Stichprobe (Sample) ist eine Teilmenge der Grundgesamtheit.
Die Grundgesamtheit (Population) ist die Gesamtheit aller Merkmalsträger, also bspw. die Gesamtheit all unserer Kunden.
Da wir nicht alle Kunden befragen können (Der Aufwand bei bspw. 5 Millionen Probanden wäre zu aufwendig), bzw. uns nicht jeder antworten wird, müssen wir uns auf eine Stichprobe dieser Grundgesamtheit beschränken.
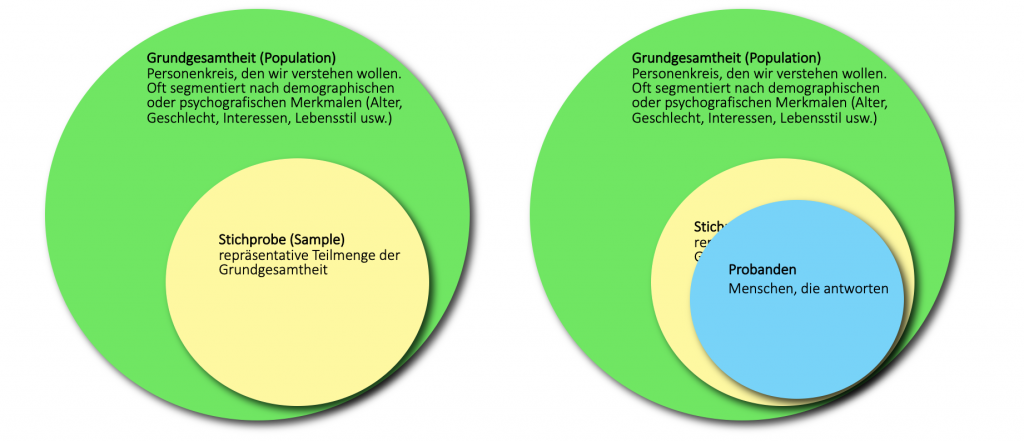 Ziel einer Stichprobe ist es, auf uns unbekannte Merkmale der Grundgesamtheit zu schließen, also eine verlässliche Hochrechnung aufstellen zu können.
Ziel einer Stichprobe ist es, auf uns unbekannte Merkmale der Grundgesamtheit zu schließen, also eine verlässliche Hochrechnung aufstellen zu können.
Ein Beispiel:
Wir haben die E-Mail-Adressen von 5 Millionen Abonnenten unseres fiktiven russischen Streaming-Dienstes “Nietflex”. Jetzt schicken wir 10.000 unserer Abonnenten eine E-Mail mit einer Aufforderung zur Teilnahme an unserer Zufriedenheitsumfrage.
Da wir aber nur 6.900 Antworten erhalten haben, fehlen uns die Meinungen der restlichen Kunden.
Bei unseren 6.900 erhaltenen Resonanzen handelt es sich also lediglich um eine Teilmenge unserer ursprünglichen Grundgesamtheit.
Jetzt fehlen uns allerdings die ganzen restlichen Kundenmeinungen, richtig?
Haben wir bei unserer Stichprobenziehung jedoch alles richtig gemacht, dann können wir auf Basis unserer Teilmenge eine verlässliche Hochrechnung aufstellen und so ein repräsentatives Bild über die Zufriedenheit all unserer 5 Millionen Kunden bekommen.
Ziel erreicht!
Wieso zufällig?
Gerade wo wir beim Thema “bei der Stichprobenziehung alles richtig machen” sind. Da stellt sich dem ein oder anderen doch die Frage, wieso wir jetzt unbedingt eine zufällige Auswahl der Probanden treffen müssen. Wäre es nicht einfacher, die ersten 100 Kunden in unserer Liste zu befragen? Hierzu schauen wir uns einmal an, was denn unsere Alternative wäre und vergleichen diese mit einer zufälligen Auswahl.
Die einzige Alternative zur zufälligen Auswahl stellt – logischerweise – die nicht zufällige Auswahl dar.
Hier gibt es mehrere nicht-zufällige Verfahren aus denen wir wählen könnten. Hierzu würden Methoden wie eine willkürliche Auswahl, bewusste Auswahl, ein Quotenplan oder ein Schneeball-Verfahren zählen. Wenn dir diese ganzen Namen nichts sagen – nicht weiter schlimm, es reicht zu wissen, wieso sie zu keinem gewünschten Ergebnis führen würden.
Knapp formuliert bieten diese Verfahren den Vorteil, dass sie günstig, schnell und unkompliziert sind oder aber einen Einblick in ganz bestimmte Eigenschaften der Grundgesamtheit liefern. Der große Nachteil ist allerdings, und das ist der springende Punkt, dass diese fehlerbehaftet und nicht verallgemeinerbar sind. Es lassen sich keine verlässlichen Hochrechnungen mit Ihnen aufstellen.
Bei einer zufälligen Auswahl dagegen lässt sich ein sogenannter Stichprobenfehler berechnen. Anhand verschiedener statistischer Verfahren lässt sich also die Genauigkeit unserer geschätzten Grundgesamtheit erfassen.
Zusammengefasst also: Nur anhand von zufällig ausgewählten Stichproben lassen sich repräsentative Umfragen erstellen. Hierfür nehmen wir uns die sogenannte einfache und die systematische Zufallsstichprobe zur Hilfe.
Voraussetzungen für die einfache und systematische Zufallsstichprobe
Mit der einfachen und der systematischen Zufallsstichprobe lässt sich also dieser Stichprobenfehler berechnen und dann mittels Hochrechnung auf die Grundgesamtheit schließen. Dazu, wie man diese genau durchführt, kommen wir gleich. Zuerst müssen wir schauen, ob hierfür alle Voraussetzungen erfüllt sind.
Ich möchte keinen mit statistischen Details langweilen, die ausführlichen Gründe aus denen die folgenden Kriterien erfüllt sein müssen, lassen sich kinderleicht googlen. Aus Gründen der Übersicht und um keinen mit der Fülle an Informationen zu erschlagen, halte ich es für angebracht, lediglich diese Checkliste abzuarbeiten:
(Voraussetzung ist z.B. eine Liste oder Kartei mit all unseren Kundendaten)
- die Listen mit den möglichen Kunden müssen durchgemischt sein (darf nicht systematisch sortiert sein)
- die Befragung (bzw. “Ziehung”) eines Kunden beeinflusst die Wahrscheinlichkeit der Befragung der anderen Kunden nicht
- es dürfen keine doppelten Einträge existieren
- die Liste muss aktuell und vollständig sein
Diese ganzen Voraussetzungen dienen dazu, dass keine Verzerrung der Grundgesamtheit entstehen kann.
Einfache Zufallsstichprobe
Haben wir uns vergewissert, dass unsere Kartei oder Liste für eine Zufallsstichprobe geeignet ist, können wir uns jetzt an den nächsten Schritt wagen. Eine sogenannte einfache Zufallsstichprobe lässt sich ganz simpel durchführen.
Zunächst müssen wir uns sicher sein, dass jeder Kunde die exakt gleiche Wahrscheinlichkeit hat befragt zu werden. Dass diese über 0 liegen muss, ist klar.
Dann geben wir jedem Element in unserer Liste stellvertretend eine Nummer.
Damit die Stichprobenauswahl auch wirklich zufällig ist, muss gewährleistet sein, dass jede mögliche Stichprobe die gleiche Wahrscheinlichkeit hat, gezogen zu werden.
Klingt etwas wirr? Kein Problem. Am anschaulichsten erklärt es sich an einem
Beispiel:
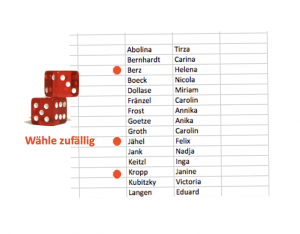
Wir sind im Karnevalsverein mit insgesamt 30 Mitgliedern und wollen zufällig 3 Leute auswählen, die sich am Tag nach Karneval um die Aufräumarbeiten kümmern. Wir möchten fair sein, also lassen wir unseren 30-Seitigen Würfel entscheiden. Du weißt schon, dieser komische Würfel der bei Dungeons & Dragons zum Einsatz kommt. Wir würfeln 3 mal und schon haben wir unsere einfache Zufallsstichprobe
Doch was machen wir, wenn wir wie in unserem “Nietflex” Beispiel 5 Millionen Leute zur Auswahl haben? Natürlich weiss jeder Mensch, der noch so wenig mit D&D zu tun hat, dass es keinen einzigen Würfel mit 5 Millionen Seiten gibt. Dafür gibt es jedoch ein Wunderwerk der Technik, sogenannte “RNG”, also Random Number Generator.
Der Computer würfelt quasi zufällig, wobei jeder einzelne unserer 5 Millionen Abonnenten die gleiche Wahrscheinlichkeit besitzt, ausgewählt zu werden.

Das war also die erste unserer Möglichkeiten. Eigentlich gar nicht so schwer.
Systematische Zufallsstichprobe
Zum Schluss fehlt uns nur noch eins: Wie führe ich eine systematische Zufallsstichprobe durch? Die systematische Zufallsstichprobe ist ähnlich unkompliziert.
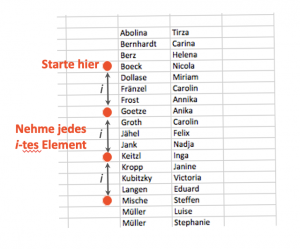
Wir bestimmen komplett zufällig (mit dem Würfel oder RNG) einen Startpunkt in unserer Liste. Der erste Schritt ist also identisch wie beim ersten “würfeln” der einfachen Zufallsstichprobe. Als nächstes bestimmen wir einen Abstand, mit dem wir von unserem Startpunkt aus unsere Kunden zur Befragung auswählen. Diesen Abstand ermitteln wir anhand der Formel “i=N/n”. Hierbei ist i unser Abstand, N die Größe der Grundgesamtheit und n die Größe der Stichprobe, die wir ziehen wollen.
Hierzu wieder ein Beispiel:
Wir nehmen uns noch einmal die Liste unseres Vereins und gehen Schritt für Schritt vor. Als erstes nehmen wir unseren zuverlässigen 30-Seitigen D&D Würfel und würfeln zum Beispiel eine 4. Unser Startpunkt ist also das vierte Mitglied auf der Liste. Wir brauchen diesmal 7 unserer Mitglieder, um mit den Aufräumarbeiten nach der Party zurecht zu kommen. Wir setzen in die Formel i=N/n also unsere Werte ein: i=30/7.
Hier kommt i = 4,29 raus, abgerundet i=4. Also ziehen wir vom Startpunkt aus jeden vierten, bis wir unsere 7 voll haben. Wir ziehen also den 8., den 12., den 16. aus der Liste und immer so weiter.

Und das wars auch schon. Mehr müssen wir gar nicht machen! Falls dich noch interessiert wie groß eine Stichprobe sein muss, um repräsentativ zu sein, gibt es auf Questionstar.de einen bequemen Stichprobenrechner.
Zusammenfassung
Hier nochmal alles wichtige in Stichpunkten zusammengefasst:
- anhand von Stichproben lässt sich durch Hochrechnungen auf Merkmale der Grundgesamtheit schließen
- Stichproben müssen zufällig sein um Repräsentativität zu gewährleisten
- dafür muss eine Liste oder Kartei mit Daten der Grundgesamtheit (z.B. Kundenliste) existieren
- diese muss bestimmte Voraussetzungen erfüllen (z.B. vollständig und aktuell sein, keine Doppeleintragungen enthalten etc.)
- für die einfache Zufallsstichprobe wird die Stichprobe komplett zufällig gewählt (es wird quasi gewürfelt), wobei bspw. jeder Kunde die gleiche Wahrscheinlichkeit besitzt ausgewählt zu werden
- bei der systematischen Zufallsstichprobe bestimmen wir zufällig einen Startpunkt in unserer Kundenliste von dem aus wir dann nur die Kunden nach einem bestimmten Abstand befragen, bspw. jeden 7.
- diesen Abstand bestimmen wir in Relation von der Stichprobengröße nach der Formel “i=N/n”
Dieser Artikel konnte etwas Licht in’s Dunkle bringen und es ist etwas klarer, weshalb man Stichproben zufällig ziehen sollte und wie man eine einfache und systematische Zufallsstichprobe zieht.
Jetzt steht keinem von uns mehr etwas im Weg, unsere eigene Umfrage zur Präsidentenwahl zu stellen. Vielleicht sogar auf Questionstar.de?
Autor:
Paul Cadenbach
Quellen
- Schumann S. (2019)., Repräsentative Umfrage: Praxisorientierte Einführung in empirische Methoden und statistische Analyseverfahren (7.Auflage), Walter de Gryuter
- Möhring W., Schlütz D. (2019), Die Befragung in der Medien- und Kommunikationswissenschaft (3.Auflage), Springer VS