5.2 Induktive Statistik: Kann man die Ergebnisse auf die Grundgesamtheit übertragen?
5.2.1 Hypothesentest
Hypothesentest
Hypothesentest ist ein fünfstufiges Verfahren, in dem basierend auf den Daten einer Stichprobe und unter Einsatz von Wahrscheinlichkeitstheorie es bestimmt wird, ob eine Hypothese hinreichend begründet ist.
M.a.W. ist dies eine Methode zu prüfen, ob die auf einer Zufallsstichprobe erhaltenen Ergebnisse sich verallgemeinern bzw. auf die Grundgesamtheit übertragen lassen.
„Menschen sind sich irrtümlicherweise zuversichtlich in ihrem Wissen und unterschätzen die Wahrscheinlichkeit, dass ihre Informationen und ihre Überzeugungen sich als falsch erweisen können. Sie neigen dazu solche zusätzliche Informationen zu suchen, die nur bestätigen, was sie schon immer gewusst haben.“
Max Bazerman
Vorgehensweise:
1.Formulierung einer Nullhypothese und ihrer Alternativhypothese
2.Festlegen vom Signifikanzniveau
3.Wahl der geeigneten Teststatistik
4.Formulierung der Entscheidungsregel
5.Berechnung von Kennzahlen aus der Stichprobe, Treffen der Entscheidung
Internetnutzung und Geschlecht
| Geschlecht | |||
| Internetnutzung | Männlich | Weiblich | Gesamt (Zeile) |
| selten | 5 | 10 | 15 |
| häufig | 10 | 5 | 15 |
| Gesamt (Spalte) | 15 | 15 | n=30 |
Ausgehend von dieser Stichprobe:
Nutzen Männer wirklich das Internet häufiger als Frauen in der Bevölkerung?
Schritt 1: Formulierung einer Nullhypothese und ihrer Alternativhypothese
H0: Es gibt keinen Unterschied zwischen Männern und Frauen im Hinblick auf die Häufigkeit der Internetnutzung.
INm=INf
H1: Männer und Frauen zeigen unterschiedliches Internetnutzungsverhalten.
INm≠INf
Nullhypothese (H0) ist eine Behauptung des Status-Quo, dass es keinen Unterschied bzw. keinen Effekt gibt.
Alternativhypothese (H1) behauptet das Gegenteil – dass es einen Unterschied bzw. einen Effekt gibt.
Schritt 2: Festlegen vom Signifikanzniveau
| Nullhypothese (H0) ist wahr |
Nullhypothese (H0) ist falsch |
|
|
Nullhypothese zurückweisen |
Fehler 1. Art |
Richtige Entscheidung True positive |
|
Nullhypothese NICHT zurückweisen |
Richtige Entscheidung |
Fehler 2. Art |
Fehler 1. Art – α – Signifikanz
Fehler 2. Art – β
(1-β) – Power
Signifikanz (α) – Wahrscheinlichkeit, dass eine wahre Nullhypothese zurückgewiesen wird.
β – Wahrscheinlichkeit, dass eine falsche Nullhypothese angenommen wird.
Analogie: Unschuld in einem Strafprozess
H0: Der Angeklagte ist unschuldig
Fehler 1. Art – (Verurteilung eines Unschuldigen)
Fehler 2. Art – (Freilassen eines Verbrechers)
Analogie: Rascheln im Gebüsch – ist das ein Löwe?
H0: Es gibt keinen Löwen im Gebüsch
Fehler 1. Art – Es gibt keinen Löwen, aber Sie laufen weg
Fehler 2. Art –Sie bleiben unbesorgt neben dem Gebüsch, der Löwe ist auf der Jagt
Signifikanzniveaus in der Marktforschung
α – Signifikanzniveau
0,01 (1%)
0,05 (5%)
(1-α) – Vertrauenswahrscheinlichkeit
0,99 (99%)
0,95 (95%)
Schritt 3: Wahl der geeigneten Teststatistik
| Stichprobe | Anwendung auf | Skalenniveaus | Teststatistiken / Kommentare |
| Eine Stichprobe | Verteilungen | Nicht-metrisch | Kolmogorow-Smirnow- und χ2-Test auf Anpassungsgüte; Runs-Test auf Zufälligkeit; Binomialtest auf Anpassungsgüte von dichotomen Variablen |
| Mittelwerte | Metrisch | t-Test, wenn Varianz ist unbekannt
z-Test, wenn Varianz ist bekannt |
|
| Proportionen | Metrisch | z-Test | |
| Zwei unabhängige Stichproben | Verteilungen | Nicht-metrisch | Kolmogorow-Smirnow-Test auf Übereinstimmung von Verteilungen für zwei Stichproben |
| Mittelwerte | Metrisch | Zweistichproben t-Test
F-Test für Gleichheit von Varianzen |
|
| Proportionen | Metrisch, Nicht-metrisch | z-Test
χ2-Test |
|
| Rangplätze / Mediane | Nicht-metrisch | Mann-Whitney-U-Test ist sensibler als Median-Test | |
| Gepaarte Stichproben | Mittelwerte | Metrisch | Paardifferenz-t-Test |
| Proportionen | Nicht-metrisch | McNemar-Test für binäre Variablen,
χ2-Test |
|
| Rangplätze / Mediane | Nicht-metrisch | Wilcoxon-Vorzeichen-Rang-Test ist sensibler als Vorzeichentest |
In unserem Beispiel haben wir es mit der Verteilung von nicht-metrischen Variablen (seltene oder häufige Internetnutzung; Männer oder Frauen) in einer Stichprobe zu tun.
χ2 (Chi-quadrat) Teststatistik auf Anpassungsgüte wird zum Test statistischer Signifikanz von dem in Kreuztabellen beobachteten Zusammenhang verwendet.
H0: Es gibt keinen Zusammenhang zwischen den Variablen
χ2 prüft dabei die Gleichheit von Häufigkeitsverteilungen.
Welche Verteilungen / Häufigkeiten müssen wir vergleichen?
fe – Häufigkeiten, die wir in den Zellen der Kreuztabelle erwarten würden, wenn es keinen Zusammenhang zwischen den Variablen gäbe.
fo – Tatsächlich beobachteten Häufigkeiten.
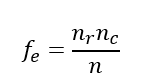
nr – Gesamtsumme in einer Zeile
nc – Gesamtsumme in einer Spalte
n – Umfang der Stichprobe
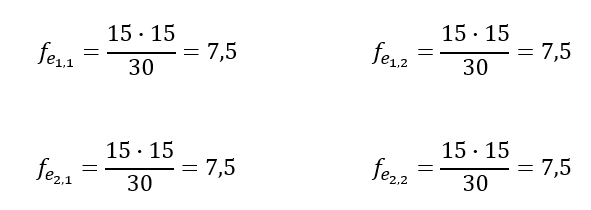
χ2-Wert sollte immer nur mit absoluten Häufigkeiten berechnet werden. Wenn Ihre Daten in Prozentform (also als relative Häufigkeiten) aufbereitet sind, müssen sie zuvor in die absolute Häufigkeiten umgerechnet werden.
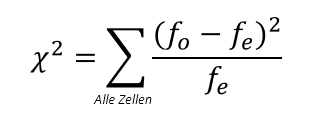
In unserem Beispiel:
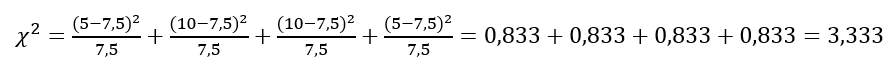
Schritt 4: Formulierung der Entscheidungsregel
TScal – beobachteter (berechneter) Wert der Teststatistik.
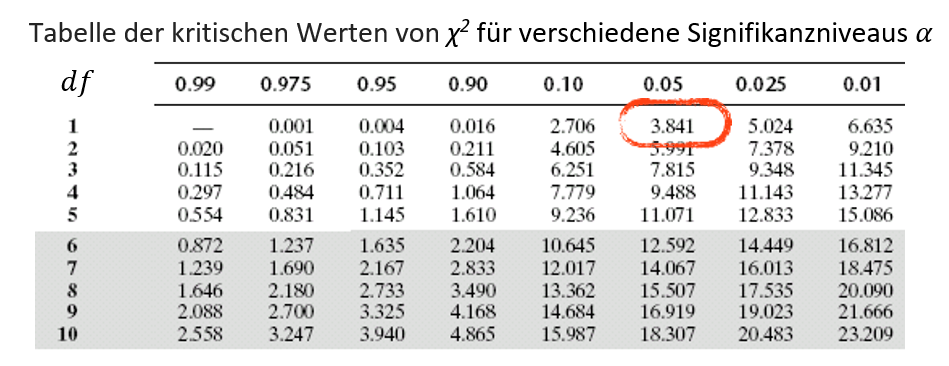
TScr – kritischer Wert der Teststatistik für gewähltes Signifikanzniveau
Wenn Wahrscheinlichkeit von TScal< Signifikanzniveau (α), dann lehne H0 ab.
oder
Wenn TScal>TScr, dann weise H0 zurück.
df=(r-1)(c-1)
df – Freiheitsgrade
r – Anzahl von Zeilen
c – Anzahl von Spalten
df=(2-1)(2-1)=1
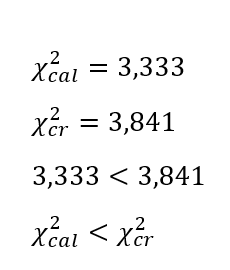
H0 kann NICHT zurückgewiesen werden
Schritt 5: Treffen der Entscheidung
Ist der Beweis da?
Was sind die Konsequenzen?
– H0, dass es keinen Zusammenhang gibt, kann nicht zurückgewiesen werden
– Zusammenhang ist statistisch nicht signifikant auf dem Signifikanzniveau von 0,05
– Die aus der Stichprobe beobachtete Ergebnisse können auf die Grundgesamtheit nicht verallgemeinert werden
Internetnutzung und Geschlecht
| Geschlecht | |||
| Internetnutzung | Männlich | Weiblich | Gesamt (Zeile) |
| selten | 5 | 10 | 15 |
| häufig | 10 | 5 | 15 |
| Gesamt (Spalte) | 15 | 15 | n=30 |
Ausgehend von dieser Stichprobe:
Nutzen Männer wirklich das Internet häufiger als Frauen in der Bevölkerung?
Antwort: Die Stichprobe erbringt dafür keine Beweise.
Wenn die Stichprobe sorgfältig ausgewählt und gezogen wurde, dann können wir behaupten, dass es mit 95%igen Vertrauenswahrscheinlichkeit keinen solchen Zusammenhang gibt.
Ansonsten – wir wissen es nicht.
