4. Stichproben
4.4 Größe der Stichprobe
Bestimmung der Stichprobegröße
Die Stichprobengröße häng nicht von der Größe der Grundgesamtheit ab, vielmehr wird sie durch qualitative Aspekte der Studie bestimmt.
- – Gewünschte Genauigkeit der Vorhersagen
- – Kenntnis über die Parameter der Grundgesamtheit
- – Anzahl von Variablen
- – Typ der Analyse
- – Wichtigkeit der Entscheidung
- – Rücklauf- und Abbruchquoten
- – Ressourceneinschränkungen

Typische Stichprobengrößen in der Marktforschung
| Typ der Studie | Minimaler Umfang | Typischer Umfang |
| Problemidentifizierungs-Studien
(z.B. Markpotenzial) |
500 | 1.000 – 2.000 |
|
Problemlösungs-Studien (z.B. Preissetzung) |
200 |
300 – 500 |
|
Produkttests |
200 |
300 – 500 |
|
Studien auf den Testmärkten |
200 |
300 – 500 |
|
TV/Radio/Print Werbung (pro Anzeige) |
150 |
200 – 300 |
|
Audit von Test-Märkten |
10 Geschäfte |
10 – 20 Geschäfte |
|
Focus-Gruppen |
6 Gruppen |
10 – 15 Gruppen |
Ansatz der Fehlerspanne zur Bestimmung vom Stichprobenumfang
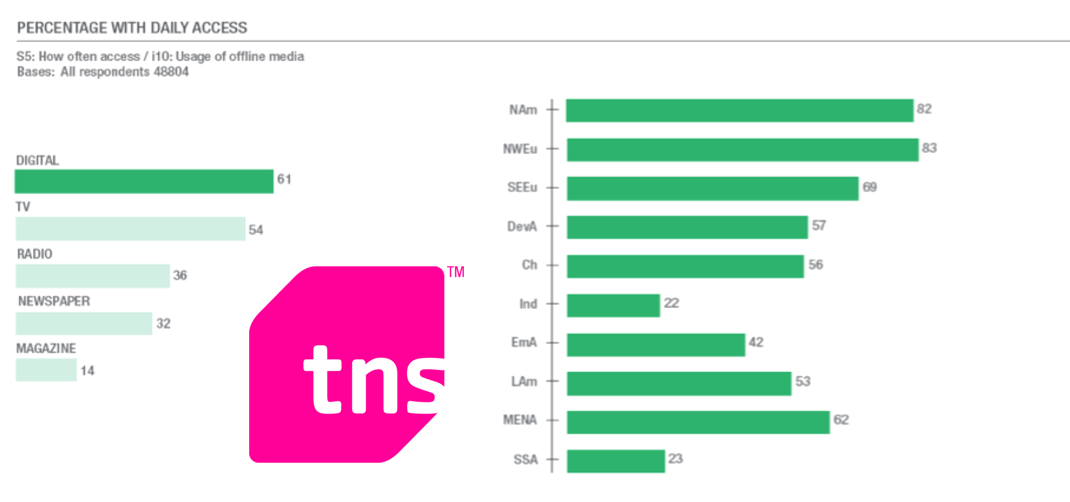
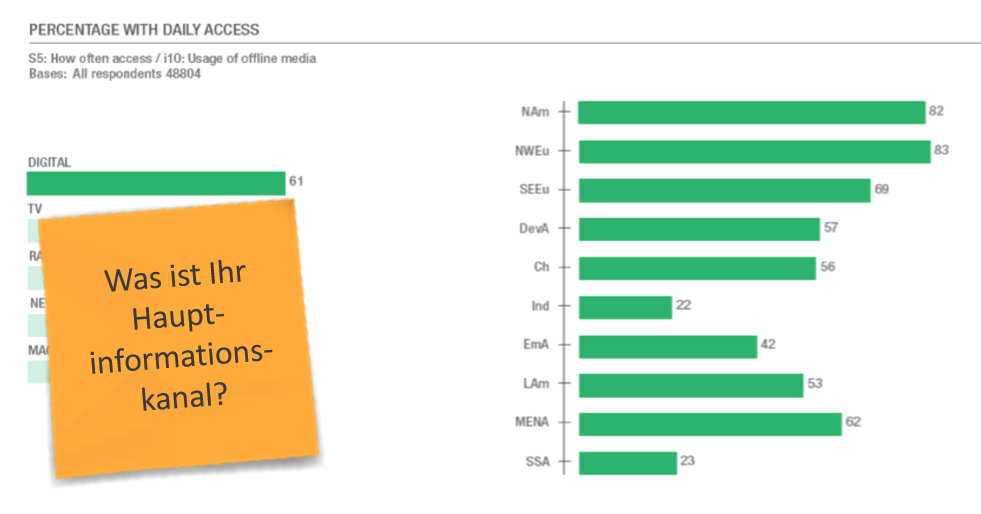
Wie genau ist diese Zahl? Wie hoch ist die Fehlerspanne?
Fehlerspanne ist das Maß der Genauigkeit einer Umfrage.
Je kleiner die Fehlerspanne, desto genauer sind die Schätzungen der Umfrage.

Mittelwerte
Nutzen Sie diese Formel zur Beurteilung der auf der Stichprobe errechneten Mittelwerte
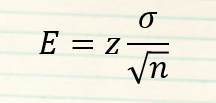
- z = z-Wert für das vorgegebene Vertrauensniveau
σ = Standardabweichung vom Parameter in der Grundgesamtheit
n = Umfang der Stichprobe
Verhältnisse
Nutzen Sie diese Formel zur Beurteilung von errechneten Verhältnissen (Proportionen)
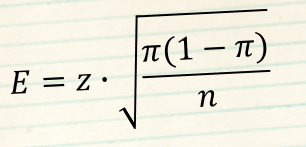
- z = z-Wert für das vorgegebene Vertrauensniveau
- π = Schätzwert für die Proportion in der Grundgesamtheit
- n = Umfang der Stichprobe
σ и π(1-π) – Meistens unbekannt
π(1-π) – Maximal bei π = 0,5
Verhältnisse
- z-Werte
- z = 1,96
- für 95% Vertrauensniveau
- z = 2,58
- für 99% Vertrauensniveau
Maximale Fehlerspanne für 95% Vertrauensniveau
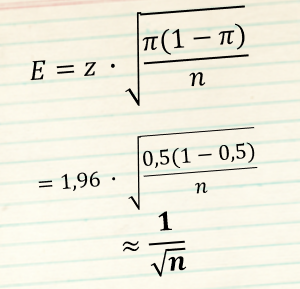
Wie genau ist diese Zahl? Wie hoch ist die Fehlerspanne?
- Fehlerspanne = 1/√n
- 48.804 Menschen in der Stichprobe
- √48.804=220,916
- 1/221 = 0,0045
- *100 = 0,45%
- ⇒ x = 61% ± 0,27% (0,27% = 0,45% von 61%)
- ⇒ 60,73% bis 61,27%
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
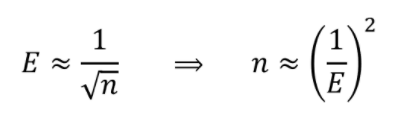
Wie groß muss die Stichprobe für die Fehlerspanne von ±1% sein?
Umfang der Stichprobe = (1/Fehlerspanne)^2
- n±1%= (1/0,01)^2 = (100)^2 = 10.000
- n±2%= (1/0,02)^2 = 502 = 2.500
- n±5%= (1/0,05)^2 = 202 = 400
- n±10%= (1/0,1)^2 = 102 = 100
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
Wenn die Stichprobe größer ist als 10% der Grundgesamtheit, sind Korrekturen notwendig
Umfang der Stichprobe = (1/Fehlerspanne)^2
Umfang der Stichprobe hängt nicht von der Grundgesamtheit ab.
- n±1%= (1/0,01)^2 = (100)^2 = 10.000
Was ist, wenn die untersuchte Grundgesamtheit nur aus 100 Elementen besteht? (z.B. Autohersteller)
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
Korrektur vom Stichprobenumfang
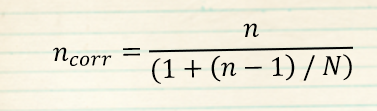
- n_corr = korrigierter Umfang der Stichprobe
- n = Umfang der Stichprobe
- N = Umfang der Grundgesamtheit
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
Fehlerspanne 1%
n±1%= (1/0,01)^2 = (100)^2 = 10.000
Was ist, wenn die untersuchte Grundgesamtheit nur aus 100 Elementen besteht? (z.B. Autohersteller)
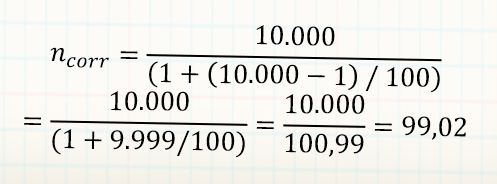
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
Fehlerspanne 5%
- n±5%= (1/0,05)^2 = (20)^2 = 400
Was ist, wenn die untersuchte Grundgesamtheit nur aus 100 Elementen besteht? (z.B. Autohersteller)
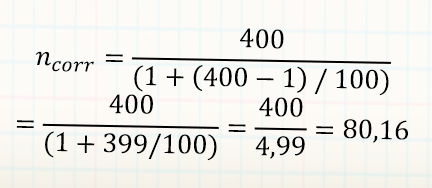
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
Fehlerspanne 10%
- n±10%= (1/0,1)^2 = (10)^2 = 100
Was ist, wenn die untersuchte Grundgesamtheit nur aus 100 Elementen besteht? (z.B. Autohersteller)
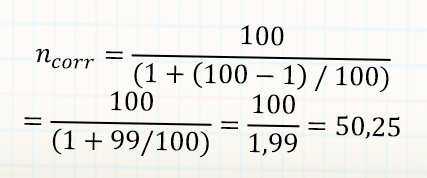
Berechnungen zeigen approximierte Werte für 95% Vertrauensniveau
Konfidenzintervall
Konfidenzintervall und Vertrauensniveau
Konfidenzintervall (Vertrauensbereich)
ist ein geschätzter Intervall von Zahlen zusammen mit Angabe der Wahrscheinlichkeit, dass dieser Intervall den unbekannten Parameterwert enthält.
Vertrauensniveau (Vertrauenswahrscheinlichkeit)
ist ein erwarteter Anteil von Intervallen, die bei einer hohen Anzahl an Stichprobenziehungen den Parameterwert enthalten werden.
Angenommen, wir möchten herausfinden, wie viele Stunden pro Tag die Mitarbeiter eines Unternehmens durchschnittlich arbeiten. Wir könnten eine Stichprobe von 30 Menschen ziehen und den Stichprobendurchschnitt von 7,5 Stunden herausfinden. Wenn wir nun sagen, dass wir uns zu 95% sicher sind, dass der echte Durchschnittswert irgendwo im Bereich von 7,2 und 7,8 Stunden liegt, sagen wir, dass wenn wir unsere Messung mit neuen Stichproben wiederholen und dabei die Fehlerspanne auf ±0,3 setzten würden, würde dieser Bereich den echten Durchschnittswert in 95% der Fälle enthalten.
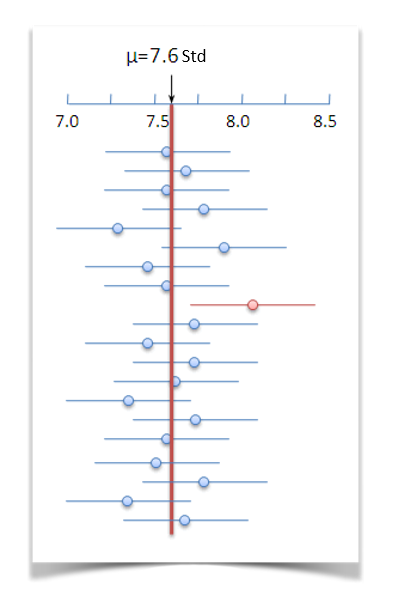
Konfidenzintervall, Fehlerspanne und Stichprobenumfang
Je höhere Sicherheit (Vertrauenswahrscheinlichkeit) wir brauchen, desto breiter wird unser Konfidenzintervall und desto höher wird unsere Fehlerspanne sein
- z-Werte
- z = 1,96
- für 95% Vertrauensniveau
- z = 2,58
- für 99% Vertrauensniveau
Maximale Fehlerspanne für 99% Vertrauensniveau
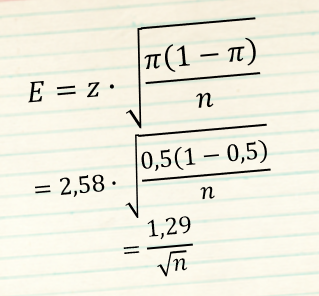
- – kleinere Fehlerspannen erfordern größere Stichproben
- – höhere Vertrauensniveaus erfordern größere Stichproben
- – Um die Fehlerspanne zu reduzieren, müssen wir den Stichprobenumfang erhöhen (√n)
