4. Stichproben
4.2 Zufällige Stichproben
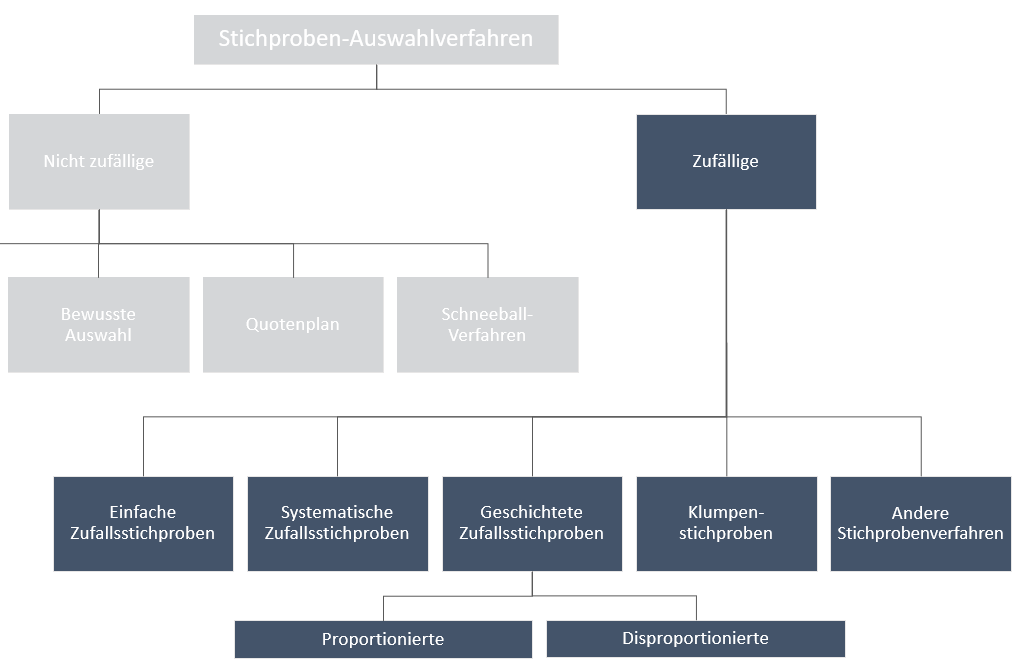
Einfache und systematische Zufallsstichproben
Erfordern Wissen über die Zusammensetzung der Grundgesamtheit.
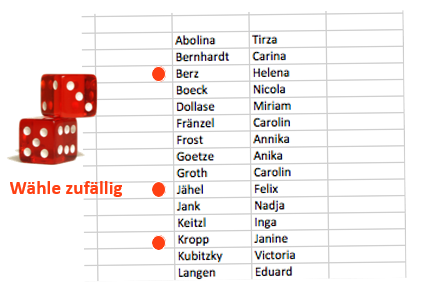
Einfache Zufallsstichproben
- – Jedes Element wird unabhängig von allen anderen Elementen ausgewählt. Das bedeutet:
- – Jedes Element der Grundgesamtheit hat eine bekannte und gleiche Wahrscheinlichkeit, ausgewählt zu werden.
- – Jede mögliche Stichprobe der gegebenen Größe(n) hat eine bekannte Wahrscheinlichkeit, tatsächlich ausgewählt zu werden.
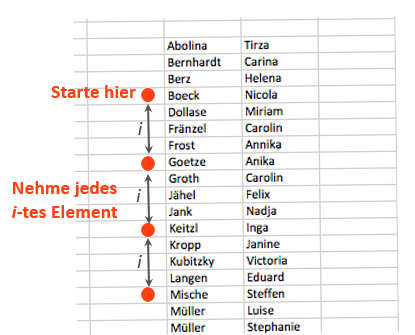
Systematische Zufallsstichproben
- – Für die Auswahl der Stichprobe wird zunächst ein „Startelement“ zufällig ausgewählt. Anschließend wird jedes i-te Element aus dem Stichprobenplan gezogen.
- – Der Abstand i ergibt sich aus der Relation des Umfangs der Grundgesamtheit N zum Umfang der Stichprobe n, d.h., i=N/n
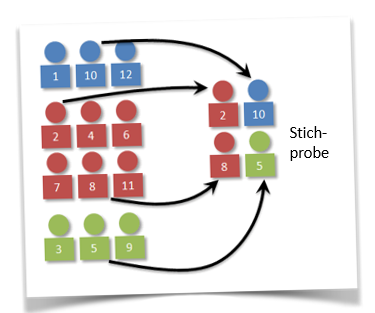
Geschichtete Zufallsstichproben
Bei der geschichteten Stichprobenziehung wird die Grundgesamtheit zunächst in die nicht-überlappenden Schichten (Stratas) aufgeteilt. Anschließend wird aus jeder Schicht ein (dis-)proportionaler Anteil der Elemente zufällig gezogen. Elemente einer Schicht müssen im gewissen Maße ähnlich sein.
Gut für:
- – Hervorheben einer bestimmten Subgruppe in der Grundgesamtheit
- – Beobachtung von Zusammenhängen und Beziehungen zwischen zwei oder mehr Subgruppen
- – Repräsentative Stichprobenziehung auch von kleinsten und unzugänglichsten Subgruppen in der Grundgesamtheit
- – höhere statistische Genauigkeit
Proportionierte
| Schicht | A | B | C |
| Umfang der Grundgesamtheit | 100 | 200 | 300 |
| Stichprobeanteil | 1/2 | 1/2 | 1/2 |
| Stichprobengröße | 50 | 100 | 150 |
Disproportionierte
| Schicht | A | B | C |
| Umfang der Grundgesamtheit | 100 | 200 | 300 |
| Stichprobeanteil | 1/5 | 1/2 | 1/3 |
| Stichprobengröße | 20 | 100 | 100 |
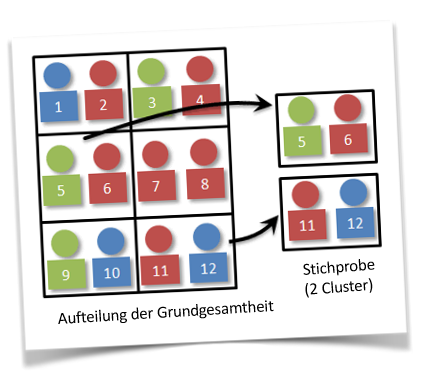
Klumpenstichproben, auch Cluster-Stichproben genannt
Bei Klumpenstichprobe wird die Grundgesamtheit zunächst in gegenseitig exklusive Klumpen (Cluster) aufgeteilt. Anschließend werden zufällig Klumpen ausgewählt, die im vollen Umfang in die Stichprobe gelangen.
Gut für:
- – Abdecken großer geographischer Gebiete
- – Reduktion von (Umfrage-)kosten
- – Wenn Konstruktion einer vollständigen Liste von Elementen der Grundgesamtheit schwierig ist
- – Wenn die Grundgesamtheit aus natürlichen Clustern besteht (z.B. Blöcke, Städte, Schulen, Krankenhäuser, Kisten usw.)